Kuta software infinite algebra 2 systems of two equations – Kuta Software Infinite Algebra 2: Systems of Two Equations – unlock the secrets to effortlessly solving simultaneous equations! This powerful software transforms the often-daunting task of solving systems of two equations into an intuitive and engaging experience. Whether you’re grappling with substitution, elimination, or graphical methods, Kuta Software provides a clear, step-by-step pathway to mastery, empowering you to conquer even the most complex algebraic challenges with confidence.
Prepare to witness the elegance of mathematical solutions unfold before your eyes, guided by this indispensable tool.
Imagine effortlessly navigating the intricacies of linear equations, visualizing solutions with clarity, and understanding the underlying principles with newfound ease. Kuta Software Infinite Algebra 2 isn’t just a program; it’s your personal tutor, your problem-solving partner, and your key to unlocking a deeper understanding of algebra. It caters to various equation types, from standard form to slope-intercept, providing immediate feedback and visual representations that bring abstract concepts to life.
Prepare to experience algebra in a whole new light.
Kuta Software Infinite Algebra 2: Mastering Systems of Two Equations: Kuta Software Infinite Algebra 2 Systems Of Two Equations
Kuta Software’s Infinite Algebra 2 is a powerful tool for students and educators alike, offering a comprehensive approach to solving various algebraic problems. Its strength lies in its ability to tackle systems of two equations, providing multiple solution methods and clear, step-by-step guidance. This article delves into the software’s capabilities, focusing on its functionalities for solving systems of two equations, highlighting its problem-solving techniques, real-world applications, and a comparison with alternative software.
Kuta Software Infinite Algebra 2: System Overview
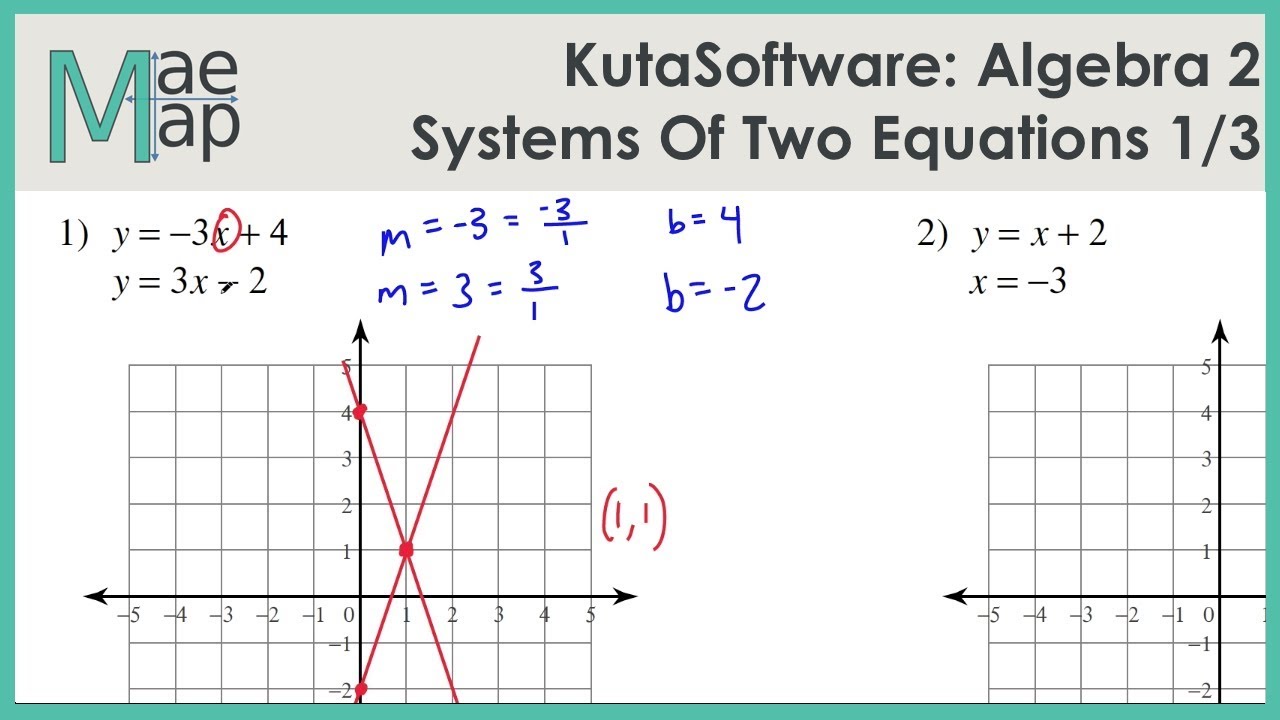
Kuta Software’s Infinite Algebra 2 provides a robust platform for solving systems of two linear equations, employing three primary methods: substitution, elimination, and graphing. Each method is meticulously detailed, allowing users to understand the underlying mathematical principles and apply them effectively. The software guides users through each step of the process, making complex algebraic manipulations more accessible.
| Method | Step 1 | Step 2 | Step 3 | Step 4 |
|---|---|---|---|---|
| Substitution | Solve one equation for one variable. | Substitute the expression from Step 1 into the other equation. | Solve the resulting equation for the remaining variable. | Substitute the value from Step 3 back into either original equation to find the value of the other variable. |
| Elimination | Multiply one or both equations by constants to make the coefficients of one variable opposites. | Add the two equations together, eliminating one variable. | Solve the resulting equation for the remaining variable. | Substitute the value from Step 3 back into either original equation to find the value of the other variable. |
| Graphing | Rewrite both equations in slope-intercept form (y = mx + b). | Graph both lines on the same coordinate plane. | Identify the point of intersection (x, y) of the two lines. This point represents the solution to the system. | Check the solution by substituting the x and y values into both original equations. |
Problem-Solving Techniques within the System
Kuta Software Infinite Algebra 2 handles various types of systems of two equations, including consistent (one solution), inconsistent (no solution), and dependent (infinitely many solutions). The software efficiently processes equations in standard form (Ax + By = C) and slope-intercept form (y = mx + b).
Interpreting the software’s output for each system type is straightforward:
- Consistent System: The software will provide a single ordered pair (x, y) representing the unique solution. This point satisfies both equations.
- Inconsistent System: The software will indicate that there is no solution. This usually manifests as parallel lines in the graphical method or a contradiction in the algebraic methods.
- Dependent System: The software will show infinitely many solutions. The equations represent the same line, meaning any point on that line satisfies both equations. The software may express this as a parametric solution.
Application of Systems of Equations

A real-world scenario perfectly suited for a system of two linear equations involves ticket sales. Let’s say a school is selling tickets for a play. Adult tickets cost $10, and student tickets cost $
5. A total of 200 tickets were sold, and the total revenue was $
1600. We can model this situation with the following system:
Let ‘a’ represent the number of adult tickets and ‘s’ represent the number of student tickets.
Equation 1: a + s = 200 (Total tickets)
Equation 2: 10a + 5s = 1600 (Total revenue)
Solving this system reveals the number of adult and student tickets sold. The solution provides meaningful results by allowing the school to understand the breakdown of ticket sales and adjust pricing or marketing strategies accordingly. A visual representation would show two intersecting lines on a graph, where the x-axis represents the number of adult tickets and the y-axis represents the number of student tickets.
The intersection point would represent the solution (a, s).
Comparing Kuta Software to Other Systems
Compared to other algebra software like Wolfram Alpha, Kuta Software Infinite Algebra 2 excels in its step-by-step approach, making the learning process more transparent. Wolfram Alpha provides concise solutions, but lacks the detailed explanations offered by Kuta Software.
| Feature | Kuta Software vs. Wolfram Alpha |
|---|---|
| Step-by-step solutions | Provides detailed steps; Wolfram Alpha offers concise results. |
| Ease of use | User-friendly interface; Wolfram Alpha requires familiarity with its input syntax. |
| Variety of solution methods | Offers substitution, elimination, and graphing; Wolfram Alpha primarily uses algebraic methods. |
Strengths of Kuta Software Infinite Algebra 2 compared to manual calculation:
- Reduces the chance of calculation errors.
- Provides a clear and organized solution process.
- Offers multiple solution methods for comparison.
Weaknesses of Kuta Software Infinite Algebra 2 compared to manual calculation:
- Reliance on technology; understanding the underlying concepts remains crucial.
- Limited in handling very complex systems or non-linear equations without advanced features.
Advanced Features and Limitations, Kuta software infinite algebra 2 systems of two equations

While Kuta Software Infinite Algebra 2 primarily focuses on linear systems, some versions might include features for handling simpler non-linear systems or matrix operations. However, its capabilities are primarily geared towards linear algebra.
Limitations of the software:
- Limited handling of non-linear systems of equations.
- Inability to solve systems with more than two equations (without using matrix methods, if available).
- Dependence on a stable internet connection (for online versions).
Mastering systems of two equations is no longer a formidable task but an achievable goal with Kuta Software Infinite Algebra 2. This software doesn’t just provide answers; it cultivates understanding. By visualizing solutions and breaking down complex problems into manageable steps, it empowers you to confidently tackle any algebraic challenge. Embrace the power of intuitive software and unlock your full algebraic potential.
Discover how craigslist pets muskegon michigan has transformed methods in this topic.
The journey to algebraic fluency starts now.